Book 2.7

Like bodies in like situations are said to be moved among themselves with like motions and in proportional times, when their situations at the end of those times are always found alike in respect of each other; as suppose we compare the particles in one system with the correspondent particles in the other. Hence the times will be proportional, in which similar and proportional parts of similar figures will be described by correspondent particles. Therefore if we suppose two systems of this kind, the correspondent particles, by reason of the similitude of the motions at their beginning, will continue to be moved with like motions, so long as they move without meeting one another; for if they are acted on by no forces,they will go on uniformly in right lines, by the 1st Law. But if they do agitate one another with some certain forces, and those forces are as the diameters of the correspondent particles inversely and the squares of the velocities directly, then, because the particles are in like situations, and their forces are proportional, the whole forces with which correspondent particles are agitated, and which are compounded of each of the agitating forces (by Corol. 2 of the Laws), will have like directions, and have the same effect as if they respected centres placed alike among the particles; and those whole forces will be to each other as the several forces which compose them, that is, as the diameters of the correspondent particles inversely, and the squares of the velocities directly: and therefore will cause correspondent particles to continue to describe like figures. These things will be so (by Cor. 1 and 8, Prop. IV., Book 1), if those centres are at rest but if they are moved, yet by reason of the similitude of the translations, their situations among the particles of the system will remain similar, so that the changes introduced into the figures described by the particles will still be similar. So that the motions of correspondent and similar particles will continue similar till their first meeting with each other; and thence will arise similar collisions, and similar reflexions; which will again beget similar motions of the particles among themselves (by what was just now shown), till they mutually fall upon one another again, and so on ad infinitum.

Cor. 1. Hence if any two bodies, which are similar and in like situations to the correspondent particles of the systems, begin to move amongst them in like manner and in proportional times, and their magnitudes and densities be to each other as the magnitudes and densities of the corresponding particles, these bodies will continue to be moved in like manner and in proportional times: for the case of the greater parts of both systems and of the particles is the very same.

Cor. 2. And if all the similar and similarly situated parts of both systems be at rest among themselves; and two of them, which are greater than the rest, and mutually correspondent in both systems, begin to move in lines alike posited, with any similar motion whatsoever, they will excite similar motions in the rest of the parts of the systems, and will continue to move among those parts in like manner and in proportional times; and will therefore describe spaces proportional to their diameters.

For the resistance arises partly from the centripetal or centrifugal forces with which the particles of the system mutually act on each other, partly from the collisions and reflexions of the particles and the greater parts. The resistances of the first kind are to each other as the whole motive forces from which they arise, that is, as the whole accelerative forces and the quantities of matter in corresponding parts; that is (by the supposition), as the squares of the velocities directly, and the distances of the corresponding particles inversely, and the quantities of matter in the correspondent parts directly: and therefore since the distances of the particles in one system are to the correspondent distances of the particles of the other as the diameter of one particle or part in the former system to the diameter of the correspondent particle or part in the other, and since the quantities of matter are as the densities of the parts and the cubes of the diameters; the resistances are to each other as the squares of the velocities and the squares of the diameters and the densities of the parts of the systems.   Q.E.D.   The resistances of the latter sort are as the number of correspondent reflexions and the forces of those reflexions conjunctly; but the number of the reflexions are to each other as the velocities of the corresponding parts directly and the spaces between their reflexions inversely. And the forces of the reflexions are as the velocities and the magnitudes and the densities of the corresponding parts conjunctly; that is, as the velocities and the cubes of the diameters and the densities of the parts. And, joining all these ratios, the resistances of the corresponding parts are to each other as the squares of the velocities and the squares of the diameters and the densities of the parts conjunctly.   Q.E.D.

Cor. 1. Therefore if those systems are two elastic fluids, like our air, and their parts are at rest among themselves; and two similar bodies proportional in magnitude and density to the parts of the fluids, and similarly situated among those parts, be any how projected in the direction of lines similarly posited; and the accelerative forces with which the particles of the fluids mutually act upon each other are as the diameters of the bodies projected inversely and the squares of their velocities directly; those bodies will excite similar motions in the fluids in proportional times, and will describe similar spaces and proportional to their diameters.

Cor. 2. Therefore in the same fluid a projected body that moves swiftly meets with a resistance that is, in the duplicate ratio of its velocity, nearly. For if the forces with which distant particles act mutually upon one another should be augmented in the duplicate ratio of the velocity, the projected body would be resisted in the same duplicate ratio accurately; and therefore in a medium, whose parts when at a distance do not act mutually with any force on one another, the resistance is in the duplicate ratio of the velocity accurately. Let there be, therefore, three mediums A, B, C, consisting of similar and equal parts regularly disposed at equal distances. Let the parts of the mediums A and B recede from each other with forces that are among themselves as T and V; and let the parts of the medium C be entirely destitute of any such forces. And if four equal bodies D, E, F, G, move in these mediums, the two first D and E in the two first A and B, and the other two F and G in the third C; and if the velocity of the body D be to the velocity of the body E, and the velocity of the body F to the velocity of the body G, in the subduplicate ratio of the force T to the force V; the resistance of the body D to the resistance of the body E, and the resistance of the body F to the resistance of the body G, will be in the duplicate ratio of the velocities; and therefore the resistance of the body D will be to the resistance of the body F as the resistance of the body E to the resistance of the body G. Let the bodies D and F be equally swift, as also the bodies E and G; and, augmenting the velocities of the bodies D and F in any ratio, and diminishing the forces of the particles of the medium B in the duplicate of the same ratio, the medium B will approach to the form and condition of the medium C at pleasure; and therefore the resistances of the equal and equally swift bodies E and G in these mediums will perpetually approach to equality so that their difference will at last become less than any given. Therefore since the resistances of the bodies D and F are to each other as the resistances of the bodies E and G, those will also in like manner approach to the ratio of equality. Therefore the bodies D and F, when they move with very great swiftness, meet with resistances very nearly equal; and therefore since the resistance of the body F is in a duplicate ratio of the velocity, the resistance of the body D will be nearly in the same ratio.

Cor. 3. The resistance of a body moving very swift in an elastic fluid is almost the same as if the parts of the fluid were destitute of their centrifugal forces, and did not fly from each other; if so be that the elasticity of the fluid arise from the centrifugal forces of the particles, and the velocity be so great as not to allow the particles time enough to act.

Cor. 4. Therefore, since the resistances of similar and equally swift bodies, in a medium whose distant parts do not fly from each other, are as the squares of the diameters, the resistances made to bodies moving with very great and equal velocities in an elastic fluid will be as the squares of the diameters, nearly.

Cor. 5. And since similar, equal, and equally swift bodies, moving through mediums of the same density, whose particles do not fly from each other mutually, will strike against an equal quantity of matter in equal times, whether the particles of which the medium consists be more and smaller, or fewer and greater, and therefore impress on that matter an equal quantity of motion, and in return (by the 3d Law of Motion) suffer an equal re-action from the same, that is, are equally resisted; it is manifest, also, that in elastic fluids of the same density, when the bodies move with extreme swiftness, their resistances are nearly equal, whether the fluids consist of gross parts, or of parts ever so subtile. For the resistance of projectiles moving with exceedingly great celerities is not much diminished by the subtilty of the medium.

Cor. 6. All these things are so in fluids whose elastic force takes its rise from the centrifugal forces of the particles. But if that force arise from some other cause, as from the expansion of the particles after the manner of wool, or the boughs of trees, or any other cause, by which the particles are hindered from moving freely among themselves, the resistance, by reason of the lesser fluidity of the medium, will be greater than in the Corollaries above.

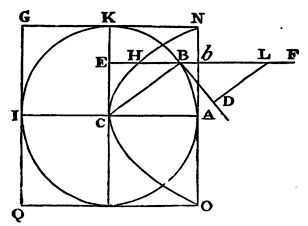
For since the action of the medium upon the body is the same (by Cor. 5 of the Laws) whether the body move in a quiescent medium, or whether the particles of the medium impinge with the same velocity upon the quiescent body, let us consider the body as if it were quiescent, and see with what force it would be impelled by the moving medium. Let, therefore, ABKI represent a spherical body described from the centre O with the semi-diameter CA, and let the particles of the medium impinge with a given velocity upon that spherical body in the directions of right lines parallel to AC; and let FB be one of those right lines. In FB take LB equal to the semi-diameter CB, and draw BD touching the sphere in B. Upon KC and BD let fall the perpendiculars BE, LD; and the force with which a particle of the medium, impinging on the globe obliquely in the direction FB, would strike the globe in B, will be to the force with which the same particle, meeting the cylinder ONGQ, described about the globe with the axis ACI, would strike it perpendicularly in b, as LD to LB, or BE to BC. Again; the efficacy of this force to move the globe, according to the direction of its incidence FB or AC, is to the efficacy of the same to move the globe, according to the direction of its determination, that is, in the direction of the right line BC in which it impels the globe directly, as BE to BC. And, joining these ratios, the efficacy of a particle, falling upon the globe obliquely in the direction of the right line FB to move the globe in the direction of its incidence, is to the efficacy of the same particle falling in the same line perpendicularly on the cylinder, to move it in the same direction, as BE² to BC². Therefore if in bE, which is perpendicular to the circular base of the cylinder NAO, and equal to the radius AC, we take bH equal to BE²
CB; then bH will be to bE as the effect of the particle upon the globe to the effect of the particle upon the cylinder. And therefore the solid which is formed by all the right lines bH will be to the solid formed by all the right lines bE as the effect of all the particles upon the globe to the effect of all the particles upon the cylinder. But the former of these solids is a paraboloid whose vertex is C, its axis CA, and latus rectum CA, and the latter solid is a cylinder circumscribing the paraboloid; and it is known that a paraboloid is half its circumscribed cylinder. Therefore the whole force of the medium upon the globe is half of the entire force of the same upon the cylinder. And therefore if the particles of the medium are at rest, and the cylinder and globe move with equal velocities, the resistance of the globe will be half the resistance of the cylinder.   Q.E.D.

By the same method other figures may be compared together as to their resistance; and those may be found which are most apt to continue their motions in resisting mediums. As if upon the circular base CEBH from the centre O, with the radius OC, and the altitude OD, one would construct a frustum CBGF of a cone, which should meet with less resistance than any other frustum constructed with the same base and altitude, and going forwards towards D in the direction of its axis: bisect the altitude OD in Q, and produce OQ to S, so that QS may be equal to QC, and S will be the vertex of the cone whose frustum is sought.

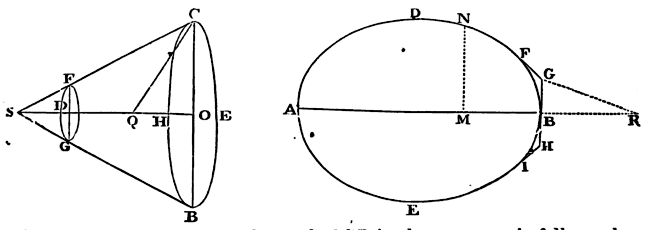
Whence, by the bye, since the angle CSB is always acute, it follows, that, if the solid ADBE be generated by the convolution of an elliptical or oval figure ADBE about its axis AB, and the generating figure be touched by three right lines FG, GH, HI, in the points P, B, and I, so that GH shall be perpendicular to the axis in the point of contact B, and FG, HI may be inclined to GH in the angles FGB, BHI of 135 degrees: the solid arising from the convolution of the figure ADFGHIE about the same axis AB will be less resisted than the former solid; if so be that both move forward in the direction of their axis AB, and that the extremity B of each go foremost. Which Proposition I conceive may be of use in the building of ships.

If the figure DNFG be such a curve, that if, from any point thereof, as N, the perpendicular NM be let fall on the axis AB, and from the given point G there be drawn the right line GR parallel to a right line touching the figure in N, and cutting the axis produced in R, MN becomes to GR as GR³ to 4BR x GB²; the solid described by the revolution of tins figure about its axis AB, moving in the before-mentioned rare medium from A towards B, will be less resisted than any other circular solid whatsoever, described of the same length and breadth.

Case 1. Let a cylinder described with the same diameter and altitude be conceived to go forward with the same velocity in the direction of its axis through the same medium; and let us suppose that the particles of the medium, on which the globe or cylinder falls, fly back with as great a force of reflexion as possible. Then since the resistance of the globe (by the last Proposition) is but half the resistance of the cylinder, and since the globe is to the cylinder as 2 to 3, and since the cylinder by falling perpendicularly on the particles, and reflecting them with the utmost force, communicates to them a velocity double to its own; it follows that the cylinder, in moving forward uniformly half the length of its axis, will communicate a motion to the particles which is to the whole motion of the cylinder as the density of the medium to the density of the cylinder; and that the globe, in the time it describes one length of its diameter in moving uniformly forward, will communicate the same motion to the particles; and in the time that it describes two thirds of its diameter, will communicate a motion to the particles which is to the whole motion of the globe as the density of the medium to the density of the globe. And therefore the globe meets with a resistance, which is to the force by which its whole motion may be either taken away or generated in the time in which it describes two thirds of its diameter moving uniformly forward, as the density of the medium to the density of the globe.

Case 2. Let us suppose that the particles of the medium incident on the globe or cylinder are not reflected; and then the cylinder falling perpendicularly on the particles will communicate its own simple velocity to them, and therefore meets a resistance but half so great as in the former case, and the globe also meets with a resistance but half so great.

Case 3. Let us suppose the particles of the medium to fly back from the globe with a force which is neither the greatest, nor yet none at all, but with a certain mean force; then the resistance of the globe will be in the same mean ratio between the resistance in the first case and the resistance in the second.   Q.E.I.

Cor. 1. Hence if the globe and the particles are infinitely hard, and destitute of all elastic force, and therefore of all force of reflexion; the resistance of the globe will be to the force by which its whole motion may be destroyed or generated, in the time that the globe describes four third parts of its diameter, as the density of the medium to the density of the globe.

Cor. 2. The resistance of the globe, caeteris paribus, is in the duplicate ratio of the velocity.

Cor. 3. The resistance of the globe, caeteris paribus, is in the duplicate ratio of the diameter.

Cor. 4. The resistance of the globe is, caeteris paribus, as the density of the medium.

Cor. 5. The resistance of the globe is in a ratio compounded of the duplicate ratio of the velocity, and the duplicate ratio of the diameter, and the ratio of the density of the medium.

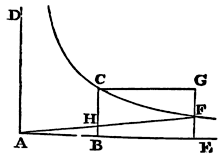
Cor. 6. The motion of the globe and its resistance may be thus expounded. Let AB be the time in which the globe may, by its resistance uniformly continued, lose its whole motion. Erect AD, BC perpendicular to AB. Let BC be that whole motion, and through the point C, the asymptotes being AD, AB, describe the hyperbola CF. Produce AB to any point E. Erect the perpendicular EF meeting the hyperbola in F. Complete the parallelogram CBEG, and draw AF meeting BC in H. Then if the globe in any time BE, with its first motion BC uniformly continued, describes in a non-resisting medium the space CBEG expounded by the area of the parallelogram, the same in a resisting medium will describe the space CBEF expounded by the area of the hyperbola; and its motion at the end of that time will be expounded by EF, the ordinate of the hyperbola, there being lost of its motion the part FG. And its resistance at the end of the same time will be expounded by the length BH, there being lost of its resistance the part CH. All these things appear by Cor. 1 and 3, Prop. V., Book II.

Cor. 7. Hence if the globe in the time T by the resistance R uniformly continued lose its whole motion M, the same globe in the time t in a resisting medium, wherein the resistance R decreases in a duplicate ratio of the velocity, will lose out of its motion M the part tM
T+t, the part TM
T+t remaining; and will describe a space which is to the space described in the same time t, with the uniform motion M, as the logarithm of the number T+t
T multiplied by the number 2,302585092994 is to the number t
T, because the hyperbolic area BCFE is to the rectangle BCGE in that proportion.

I have exhibited in this Proposition the resistance and retardation of spherical projectiles in mediums that are not continued, and shewn that this resistance is to the force by which the whole motion of the globe may be destroyed or produced in the time in which the globe can describe two thirds of its diameter; with a velocity uniformly continued, as the density of the medium to the density of the globe, if so be the globe and the particles of the medium be perfectly elastic, and are endued with the utmost force of reflexion; and that this force, where the globe and particles of the medium are infinitely hard and void of any reflecting force, is diminished one half. But in continued mediums, as water, hot oil, and quicksilver, the globe as it passes through them does not immediately strike against all the particles of the fluid that generate the resistance made to it, but presses only the particles that lie next to it, which press the particles beyond, which press other particles, and so on; and in these mediums the resistance is diminished one other half. A globe in these extremely fluid mediums meets with a resistance that is to the force by which its whole motion may be destroyed or generated in the time wherein it can describe, with that motion uniformly continued, eight third parts of its diameter, as the density of the medium to the density of the globe. This I shall endeavour to shew in what follows.

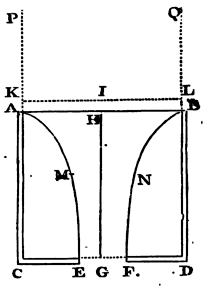
Let ACDB be a cylindrical vessel, AB the mouth of it, CD the bottom parallel to the horizon, EF a circular hole in the middle of the bottom, G the centre of the hole, and GH the axis of the cylinder perpendicular to the horizon. And suppose a cylinder of ice APQB to be of the same breadth with the cavity of the vessel, and to have the same axis, and to descend perpetually with an uniform motion, and that its parts, as soon as they touch the superficies AB, dissolve into water, and flow down by their weight into the vessel, and in their fall compose the cataract or column of water ABNFEM, passing through the hole EF, and filling up the same exactly. Let the uniform velocity of the descending ice and of the contiguous water in the circle AB be that which the water would acquire by falling through the space IH; and let IH and HG lie in the same right line; and through the point I let there be drawn the right line KL parallel to the horizon and meeting the ice on both the sides thereof in K and L. Then the velocity of the water running out at the hole EF will be the same that it would acquire by falling from I through the space IG. Therefore, by Galileo's Theorems, IG will be to IH in the duplicate ratio of the velocity of the water that runs out at the hole to the velocity of the water in the circle AB, that is, in the duplicate ratio of the circle AB to the circle EF; those circles being reciprocally as the velocities of the water which in the same time and in equal quantities passes severally through each of them, and completely fills them both. We are now considering the velocity with which the water tends to the plane of the horizon. But the motion parallel to the same, by which the parts of the falling water approach to each other, is not here taken notice of; since it is neither produced by gravity, nor at all changes the motion perpendicular to the horizon which the gravity produces. We suppose, indeed, that the parts of the water cohere a little, that by their cohesion they may in falling approach to each other with motions parallel to the horizon in order to form one single cataract, and to prevent their being divided into several: but the motion parallel to the horizon arising from this cohesion does not come under our present consideration.

Case 1. Conceive now the whole cavity in the vessel, which encompasses the falling water ABNFEM, to be full of ice, so that the water may pass through the ice as through a funnel. Then if the water pass very near to the ice only, without touching it; or, which is the same thing, if by reason of the perfect smoothness of the surface of the ice, the water, though touching it, glides over it with the utmost freedom, and without the least resistance; the water will run through the hole EF with the same velocity as before, and the whole weight of the column of water ABNFEM will be all taken up as before in forcing out the water, and the bottom of the vessel will sustain the weight of the ice encompassing that column.

Let now the ice in the vessel dissolve into water; yet will the efflux of the water remain, as to its velocity, the same as before. It will not be less, because the ice now dissolved will endeavour to descend; it will not be greater, because the ice, now become water, cannot descend without hindering the descent of other water equal to its own descent. The same force ought always to generate the same velocity in the effluent water.

But the hole at the bottom of the vessel, by reason of the oblique motions of the particles of the effluent water, must be a little greater than before. For now the particles of the water do not all of them pass through the hole perpendicularly, but, flowing down on all parts from the sides of the vessel, and converging towards the hole, pass through it with oblique motions; and in tending downwards meet in a stream whose diameter is a little smaller below the hole than at the hole itself; its diameter being to the diameter of the hole as 5 to 6, or as 5½ to 6½, very nearly, if I took the measures of those diameters right. I procured a very thin flat plate, having a hole pierced in the middle, the diameter of the circular hole being 5
8 parts of an inch. And that the stream of running waters might not be accelerated in falling, and by that acceleration become narrower, I fixed this plate not to the bottom, but to the side of the vessel, so as to make the water go out in the direction of a line parallel to the horizon. Then, when the vessel was full of water, I opened the hole to let it run out; and the diameter of the stream, measured with great accuracy at the distance of about half an inch from the hole, was 21
40 of an inch. Therefore the diameter of this circular hole was to the diameter of the stream very nearly as 25 to 21. So that the water in passing through the hole converges on all sides, and, after it has run out of the vessel, becomes smaller by converging in that manner, and by becoming smaller is accelerated till it comes to the distance of half an inch from the hole, and at that distance flows in a smaller stream and with greater celerity than in the hole itself, and this in the ratio of 25 x 25 to 21 x 21, or 17 to 12, very nearly; that is, in about the subduplicate ratio of 2 to 1. Now it is certain from experiments, that the quantity of water running out in a given time through a circular hole made in the bottom of a vessel is equal to the quantity, which, flowing with the aforesaid velocity, would run out in the same time through another circular hole, whose diameter is to the diameter of the former as 21 to 25. And therefore that running water in passing through the hole itself has a velocity downwards equal to that which a heavy body would acquire in falling through half the height of the stagnant water in the vessel, nearly. But, then, after it has run out, it is still accelerated by converging, till it arrives at a distance from the hole that is nearly equal to its diameter, and acquires a velocity greater than the other in about the subduplicate ratio of 2 to 1; which velocity a heavy body would nearly acquire by falling through the whole height of the stagnant water in the vessel.

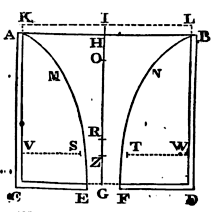
Therefore in what follows let the diameter of the stream be represented by that lesser hole which we called EF. And imagine another plane VW above the hole EF, and parallel to the plane there of, to be placed at a distance equal to the diameter of the same hole, and to be pierced through with a greater hole ST, of such a magnitude that a stream which will exactly fill the lower hole EF may pass through it; the diameter of which hole will therefore be to the diameter of the lower hole as 25 to 21, nearly. By this means the water will run perpendicularly out at the lower hole; and the quantity of the water running out will be, according to the magnitude of this last hole, the same, very nearly, which the solution of the Problem requires. The space included between the two planes and the falling stream may be considered as the bottom of the vessel. But, to make the solution more simple and mathematical, it is better to take the lower plane alone for the bottom of the vessel, and to suppose that the water which flowed through the ice as through a funnel, and ran out of the vessel through the hole EF made in the lower plane, preserves its motion continually, and that the ice continues at rest. Therefore in what follows let ST be the diamter of a circular hole described from the centre Z, and let the stream run out of the vessel through that hole, when the water in the vessel is all fluid. And let EF be the diameter of the hole, which the stream, in falling through, exactly fills up, whether the water runs out of the vessel by that upper hole ST, or flows through the middle of the ice in the vessel, as through a funnel. And let the diameter of the upper hole ST be to the diameter of the lower EF as about 25 to 21, and let the perpendicular distance between the planes of the holes be equal to the diameter of the lesser hole EF. Then the velocity of the water downwards, in running out of the vessel through the hole ST, will be in that hole the same that a body may acquire by falling from half the height IZ; and the velocity of both the falling streams will be in the hole EF, the same which a body would acquire by falling from the whole height IG.

Case 2. If the hole EF be not in the middle of the bottom of the vessel, but in some other part thereof, the water will still run out with the same velocity as before, if the magnitude of the hole be the same. For though an heavy body takes a longer time in descending to the same depth, by an oblique line, than by a perpendicular line, yet in both cases it acquires in its descent the same velocity; as Galileo has demonstrated.

Case 3. The velocity of the water is the same when it runs out through a hole in the side of the vessel. For if the hole be small, so that the interval between the superficies AB and KL may vanish as to sense, and the stream of water horizontally issuing out may form a parabolic figure: from the latus rectum of this parabola may be collected, that the velocity of the effluent water is that which a body may acquire by falling the height IG or HG of the stagnant water in the vessel. For, by making an experiment, I found that if the height of the stagnant water above the hole were 20 inches, and the height of the hole above a plane parallel to the horizon were also 20 inches, a stream of water springing out from thence would fall upon the plane, at the distance of 37 inches, very nearly, from a perpendicular let fall upon that plane from the hole. For without resistance the stream would have fallen upon the plane at the distance of 40 inches, the latus rectum of the parabolic stream being 80 inches.

Case 4. If the effluent water tend upward, it will still issue forth with the same velocity. For the small stream of water springing upward; ascends with a perpendicular motion to GH or GI, the height of the stagnant water in the vessel; excepting in so far as its ascent is hindered a little by the resistance of the air; and therefore it springs out with the same velocity that it would acquire in falling from that height. Every particle of the stagnant water is equally pressed on all sides (by Prop. XIX., Book II), and, yielding to the pressure, tends always with an equal force, whether it descends through the hole in the bottom of the vessel, or gushes out in an horizontal direction through a hole in the side, or passes into a canal, and springs up from thence through a little hole made in the upper part of the canal. And it may not only be collected from reasoning, but is manifest also from the well-known experiments just mentioned, that the velocity with which the water runs out is the very same that is assigned in this Proposition.

Case 5. The velocity of the effluent water is the same, whether the figure of the hole be circular, or square, or triangular, or any other figure equal to the circular; for the velocity of the effluent water does not depend upon the figure of the hole, but arises from its depth below the plane KL.

Case 6. If the lower part of the vessel ABDC be immersed into stagnant water, and the height of the stagnant water above the bottom of the vessel be GR, the velocity with which the water that is in the vessel will run out at the hole EF into the stagnant water will be the same which the water would acquire by falling from the height IR; for the weight of all the water in the vessel that is below the superficies of the stagnant water will be sustained in equilibrio by the weight of the stagnant water, and therefore does riot at all accelerate the motion of the descending water in the vessel. This case will also appear by experiments, measuring the times in which the water will run out.

Cor. 1. Hence if CA the depth of the water be produced to K, so that AK may be to CK in the duplicate ratio of the area of a hole made in any part of the bottom to the area of the circle AB, the velocity of the effluent water will be equal to the velocity which the water would acquire by falling from the height KC.

Cor. 2. And the force with which the whole motion of the effluent water may be generated is equal to the weight of a cylindric column of water, whose base is the hole EF, and its altitude 2GI or 2CK. For the effluent water, in the time it becomes equal to this column, may acquire, by falling by its own weight from the height GI, a velocity equal to that with which it runs out.

Cor. 3. The weight of all the water in the vessel ABDC is to that part of the weight which is employed in forcing out the water as the sum of the circles AB and EF to twice the circle EF. For let IO be a mean proportional between IH and IG, and the water running out at the hole EF will, in the time that a drop falling from I would describe the altitude IG, become equal to a cylinder whose base is the circle EF and its altitude 2IG, that is, to a cylinder whose base is the circle AB, and whose altitude is 2IO. For the circle EF is to the circle AB in the subduplicate ratio of the altitude IH to the altitude IG; that is, in the simple ratio of the mean proportional IO to the altitude IG. Moreover, in the time that a drop falling from I can describe the altitude IH, the water that runs out will hare become equal to a cylinder whose base is the circle AB, and its altitude 2IH; and in the time that a drop falling from I through H to G describes HG, the difference of the altitudes, the effluent water, that is, the water contained within the solid ABNFEM, will be equal to the difference of the cylinders, that is, to a cylinder whose base is AB, and its altitude 2HO. And therefore all the water contained in the vessel ABDC is to the whole falling water contained in the said solid ABNFEM as HG to 2HO, that is, as HO + OG to 2HO, or IH + IO to 2IH. But the weight of all the water in the solid ABNFEM is employed in forcing out the water: and therefore the weight of all the water in the vessel is to that part of the weight that is employed in forcing out the water as IH + IO to 2IH, and therefore as the sum of the circles EF and AB to twice the circle EF.

Cor. 4. And hence the weight of all the water in the vessel ABDC is to the other part of the weight which is sustained by the bottom of the vessel as the sum of the circles AB and EF to the difference of the same circles.

Cor. 5. And that part of the weight which the bottom of the vessel sustains is to the other part of the weight employed in forcing out the water as the difference of the circles AB and EF to twice the lesser circle EF, or as the area of the bottom to twice the hole.

Cor. 6. That part of the weight which presses upon the bottom is to the whole weight of the water perpendicularly incumbent thereon as the circle AB to the sum of the circles AB and EF, or as the circle AB to the excess of twice the circle AB above the area of the bottom. For that part of the weight which presses upon the bottom is to the weight of the whole water in the vessel as the difference of the circles AB and EF to the sum of the same circles (by Cor. 4); and the weight of the whole water in the vessel is to the weight of the whole water perpendicularly incumbent on the bottom as the circle AB to the difference of the circles AB and EF. Therefore, ex aequo perturbatè, that part of the weight which presses upon the bottom is to the weight of the whole water perpendicularly incumbent thereon as the circle AB to the sum of the circles AB and EF, or the excess of twice the circle AB above the bottom.

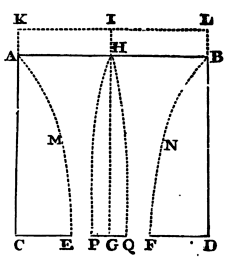
Cor. 7. If in the middle of the hole EF there be placed the little circle PQ described about the centre G, and parallel to the horizon, the weight of water which that little circle sustains is greater than the weight of a third part of a cylinder of water whose base is that little circle and its height GH. For let ABNFEM be the cataract or column of falling water whose axis is GH, as above, and let all the water, whose fluidity is not requisite for the ready and quick descent of the water, be supposed to A be congealed, as well round about the cataract, as above the little circle. And let PHQ be the column of water congealed above the little circle, whose vertex is H, and its altitude GH. And suppose this cataract to fall with its whole weight downwards, and not in the least to lie against or to press PHQ, but to glide freely by it without any friction, unless, perhaps, just at the very vertex of the ice, where the cataract at the beginning of its fall may tend to a concave figure. And as the congealed water AMEC, BNFD, lying round the cataract, is convex in its internal superficies AME, BNF, towards the falling cataract, so this column PHQ will be convex towards the cataract also, and will therefore be greater than a cone whose base is that little circle PQ and its altitude GH; that is, greater than a third part of a cylinder described with the same base and altitude. Now that little circle sustains the weight of this column, that is, a weight greater than the weight of the cone, or a third part of the cylinder.

Cor. 8. The weight of water which the circle PQ, when very small, sustains, seems to be less than the weight of two thirds of a cylinder of water whose base is that little circle, and its altitude HG. For, things standing as above supposed, imagine the half of a spheroid described whose base is that little circle, and its semi-axis or altitude HG. This figure will be equal to two thirds of that cylinder, and will comprehend within it the column of congealed water PHQ, the weight of which is sustained by that little circle. For though the motion of the water tends directly downwards, the external superficies of that column must yet meet the base PQ in an angle somewhat acute, because the water in its fall is perpetually accelerated, and by reason of that acceleration become narrower. Therefore, since that angle is less than a right one, this column in the lower parts thereof will lie within the hemi-spheroid. In the upper parts also it will be acute or pointed; because to make it otherwise, the horizontal motion of the water must be at the vertex infinitely more swift than its motion towards the horizon. And the less this circle PQ is, the more acute will the vertex of this column be; and the circle being diminished in infinitum the angle PHQ will be diminished in infinitum, and therefore the column will lie within the hemi-spheroid. Therefore that column is less than that hemi-spheroid, or than two-third parts of the cylinder whose base is that little circle, and its altitude GH. Now the little circle sustains a force of water equal to the weight of this column, the weight of the ambient water being employed in causing its efflux out at the hole.

Cor. 9. The weight of water which the little circle PQ sustains, when it is very small, is very nearly equal to the weight of a cylinder of water whose base is that little circle, and its altitude ½GH; for this weight is an arithmetical mean between the weights of the cone and the hemi-spheroid above mentioned. But if that little circle be not very small, but on the contrary increased till it be equal to the hole EF, it will sustain the weight of all the water lying perpendicularly above it, that is, the weight of a cylinder of water whose base is that little circle, and its altitude GH.

Cor. 10. And (as far as I can judge) the weight which this little circle sustains is always to the weight of a cylinder of water whose base is that little circle, and its altitude ½GH, as EF² to EF² − ½PQ², or as the circle EF to the excess of this circle above half the little circle PQ, very nearly.

For the sides are not at all opposed to the motion; and a cylinder becomes a circle when its length is diminished in infinitum.

For let the vessel ABDC touch the surface of stagnant water with its bottom CD, and let the water run out of this vessel into the stagnant water through the cylindric canal EFTS perpendicular co the horizon; and let the little circle PQ be placed parallel to the horizon any where in the 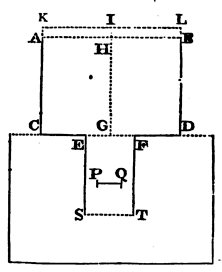middle of the canal; and produce CA to K, so that AK may be to CK in the duplicate of the ratio, which the excess of the orifice of the canal EF above the little circle PQ bears to the circle AB. Then it is manifest (by Case 5, Case 6, and Cor. 1, Prop. XXXVI) that the velocity of the water passing through the annular space between the little circle and the sides of the vessel will be the very same which the water would acquire by falling, and in its fall describing the altitude KC or IG.

And (by Cor. 10, Prop. XXXVI) if the breadth of the vessel be infinite, so that the lineola HI may vanish, and the altitudes IG, HG become equal; the force of the water that flows down and presses upon the circle will be to the weight of a cylinder whose base is that little circle, and the altitude ½IG, as EF² to EF² − ½PQ², very nearly. For the force of the water flowing downward uniformly through the whole canal will be the same upon the little circle PQ in whatsoever part of the canal it be placed.

Let now the orifices of the canal EF, ST be closed, and let the little circle ascend in the fluid compressed on every side, and by its ascent let it oblige the water that lies above it to descend through the annular space between the little circle and the sides of the canal. Then will the velocity of the ascending little circle be to the velocity of the descending water as the difference of the circles EF and PQ, is to the circle PQ; and the velocity of the ascending little circle will be to the sum of the velocities, that is, to the relative velocity of the descending water with which it passes by the little circle in its ascent, as the difference of the circles EF and PQ to the circle EF, or as EF² − PQ² to EF². Let that relative velocity be equal to the velocity with which it was shewn above that the water would pass through the annular space, if the circle were to remain unmoved, that is, to the velocity which the water would acquire by falling, and in its fall describing the altitude IG; and the force of the water upon the ascending circle will be the same as before (by Cor. 5, of the Laws of Motion); that is, the resistance of the ascending little circle will be to the weight of a cylinder of water whose base is that little circle, and its altitude ½IG, as EF² to EF² − ½PQ², nearly. But the velocity of the little circle will be to the velocity which the water acquires by falling, and in its fall describing the altitude IG, as EF² − PQ² to EF² .

Let the breadth of the canal be increased in infinitum; and the ratios between EF² − PQ² and EF², and between EF² and EF² − ½PQ², will become at last ratios of equality. And therefore the velocity of the little circle will now be the same which the water would acquire in falling, and in its fall describing the altitude IG: and the resistance will become equal to the weight of a cylinder whose base is that little circle, and its altitude half the altitude IG, from which the cylinder must fall to acquire the velocity of the ascending circle; and with this velocity the cylinder in the time of its fall will describe four times its length. But the resistance of the cylinder moving forward with this velocity in the direction of its length is the same with the resistance of the little circle (by Lem. IV), and is therefore nearly equal to the force by which its motion may be generated while it describes four times its length.

If the length of the cylinder be augmented or diminished, its motion, and the time in which it describes four times its length, will be augmented or diminished in the same ratio, and therefore the force by which the motion so increased or diminished, may be destroyed or generated, will continue the same; because the time is increased or diminished in the same proportion; and therefore that force remains still equal to the resistance of the cylinder, because (by Lem. IV) that resistance will also remain the same.

If the density of the cylinder be augmented or diminished, its motion, and the force by which its motion may be generated or destroyed in the same time, will be augmented or diminished in the same ratio. Therefore the resistance of any cylinder whatsoever will be to the force by which its whole motion may be generated or destroyed, in the time during which it moves four times its length, as the density of the medium to the density of the cylinder, nearly.   Q.E.D.

A fluid must be compressed to become continued; it must be continued and non-elastic, that all the pressure arising from its compression may be propagated in an instant; and so, acting equally upon all parts of the body moved, may produce no change of the resistance. The pressure arising from the motion of the body is spent in generating a motion in the parts of the fluid, and this creates the resistance. But the pressure arising from the compression of the fluid, be it ever so forcible, if it be propagated in an instant, generates no motion in the parts of a continued fluid, produces no change at all of motion therein; and therefore neither augments nor lessens the resistance. This is certain, that the action of the fluid arising from the compression cannot be stronger on the hinder parts of the body moved than on its fore parts, and therefore cannot lessen the resistance described in this proposition. And if its propagation be infinitely swifter than the motion of the body pressed, it will not be stronger on the fore parts than on the hinder parts. But that action will be infinitely swifter, and propagated in an instant, if the fluid be continued and non-elastic.

Cor. 1. The resistances, made to cylinders going uniformly forward in the direction of their lengths through continued infinite mediums are in a ratio compounded of the duplicate ratio of the velocities and the duplicate ratio of the diameters, and the ratio of the density of the mediums.

Cor. 2. If the breadth of the canal be not infinitely increased but the cylinder go forward in the direction of its length through an included quiescent medium, its axis all the while coinciding with the axis of the canal, its resistance will be to the force by which its whole motion, in the time in which it describes four times its length, may be generated or destroyed, in a ratio compounded of the ratio of EF² to EF² − ½PQ² once, and the ratio of EF² to EF² − PQ² twice, and the ratio of the density of the medium to the density of the cylinder.

Cor. 3. The same thing supposed, and that a length L is to the quadruple of the length of the cylinder in a ratio compounded of the ratio EF² − ½PQ² to EF² once, and the ratio of EF² − PQ² to EF² twice; the resistance of the cylinder will be to the force by which its whole motion, in the time during which it describes the length L, may be destroyed or generated, as the density of the medium to the density of the cylinder.

In this proposition we have investigated that resistance alone which arises from the magnitude of the transverse section of the cylinder, neglecting that part of the same which may arise from the obliquity of the motions. For as, in Case 1, of Prop. XXXVI., the obliquity of the motions with which the parts of the water in the vessel converged on every side to the hole EF hindered the efflux of the water through the hole, so, in this Proposition, the obliquity of the motions, with which the parts of the water, pressed by the antecedent extremity of the cylinder, yield to the pressure, and diverge on all sides, retards their passage through the places that lie round that antecedent extremity, toward the hinder parts of the cylinder, and causes the fluid to be moved to a greater distance; which increases the resistance, and that in the same ratio almost in which it diminished the efflux of the water out of the vessel, that is, in the duplicate ratio of 25 to 21, nearly. And as, in Case 1, of that Proposition, we made the parts of the water pass through the hole EF perpendicularly and in the greatest plenty, by supposing all the water in the vessel lying round the cataract to be frozen, and that part of the water whose motion was oblique, and useless to remain without motion, so in this Proposition, that the obliquity of the motions may be taken away, and the parts of the water may give the freest passage to the cylinder, by yielding to it with the most direct and quick motion possible, so that only so much resistance may remain as arises from the magnitude of the transverse section, and which is incapable of diminution, unless by diminishing the diameter of the cylinder; we must conceive those parts of the fluid whose motions are oblique and useless, and produce resistance, to be at rest among themselves at both extremities of the cylinder, and there to cohere, and be joined to the cylinder. 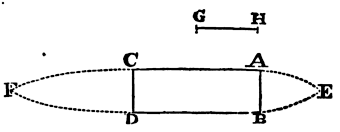Let ABCD be a rectangle, and let AE and BE be two parabolic arcs, described with the axis AB, and with a latus rectum that is to the space HG, which must be described by the cylinder in falling, in order to acquire the velocity with which it moves, as HG to ½AB. Let CF and DF be two other parabolic arcs described with the axis CD, and a latus rectum quadruple of the former; and by the convolution of the figure about the axis EF let there be generated a solid, whose middle part ABDC is the cylinder we are here speaking of, and whose extreme parts ABE and CDF contain the parts of the fluid at rest among themselves, and concreted into two hard bodies, adhering to the cylinder at each end like a head and tail. Then if this solid EACFDB move in the direction of the length of its axis FE toward the parts beyond E, the resistance will be the same which we have here determined in this Proposition, nearly; that is, it will have the same ratio to the force with which the whole motion of the cylinder may be destroyed or generated, in the time that it is describing the length 4AC with that motion uniformly continued, as the density of the fluid has to the density of the cylinder, nearly. And (by Cor. 7, Prop. XXXVI) the resistance must be to this force in the ratio of 2 to 3, at the least.

For the spaces lying between the sides of the canal, and the cylinder, sphere, and spheroid, through which the water passes, are equal; and the water will pass equally through equal spaces.

This is true, upon the supposition that all the water above the cylinder, sphere, or spheroid, whose fluidity is not necessary to make the passage of the water the quickest possible, is congealed, as was explained above in Cor. 7, Prop. XXXVI.

This appears by Lem. V and the third Law. For the water and the bodies act upon each other mutually and equally.

This appears from the last Lemma, for the relative motions remain the same among themselves.

The case is the same of all convex and round bodies, whose axes coincide with the axis of the canal. Some difference may arise from a greater or less friction; but in these Lemmata we suppose the bodies to be perfectly smooth, and the medium to be void of all tenacity and friction; and that those parts of the fluid which by their oblique and superfluous motions may disturb, hinder, and retard the flux of the water through the canal, are at rest among themselves; being fixed like water by frost, and adhering to the fore and hinder parts of the bodies in the manner explained in the Scholium of the last Proposition; for in what follows we consider the very least resistance that round bodies described with the greatest given transverse sections can possibly meet with.

Bodies swimming upon fluids, when they move straight forward, cause the fluid to ascend at their fore parts and subside at their hinder parts, especially if they are of an obtuse figure; and thence they meet with a little more resistance than if they were acute at the head and tail. And bodies moving in elastic fluids, if they are obtuse behind and before, condense the fluid a little more at their fore parts, and relax the same at their hinder parts; and therefore meet also with a little more resistance than if they were acute at the head and tail. But in these Lemmas and Propositions we are not treating of elastic but non-elastic fluids; not of bodies floating on the surface of the fluid, but deeply immersed therein. And when the resistance of bodies in non-elastic fluids is once known, we may then augment this resistance a little in elastic fluids, as our air; and in the surfaces of stagnating fluids, as lakes and seas.

Cor. 1. The resistances of globes in infinite compressed mediums are in a ratio compounded of the duplicate ratio of the velocity, and the duplicate ratio of the diameter, and the ratio of the density of the mediums.

Cor. 2. The greatest velocity, with which a globe can descend by its comparative weight through a resisting fluid, is the same which it may acquire by falling with the same weight, and without any resistance, and in its fall describing a space that is, to four third parts of its diameter as the density of the globe to the density of the fluid. For the globe in the time of its fall, moving with the velocity acquired in falling, will describe a space that will be to eight third parts of its diameter as the density of the globe to the density of the fluid; and the force of its weight which generates this motion will be to the force that can generate the same motion, in the time that the globe describes eight third parts of its diameter, with the same velocity as the density of the fluid to the density of the globe; and therefore (by this Proposition) the force of weight will be equal to the force of resistance, and therefore cannot accelerate the globe.

Cor. 3. If there be given both the density of the globe and its velocity at the beginning of the motion, and the density of the compressed quiescent fluid in which the globe moves, there is given at any time both the velocity of the globe and its resistance, and the space described by it (by Cor. 7, Prop. XXXV).

Cor. 4. A globe moving in a compressed quiescent fluid of the same density with itself will lose half its motion before it can describe the length of two of its diameters (by the same Cor. 7).

In the last two Propositions we suppose (as was done before in Lem. V) that all the water which precedes the globe, and whose fluidity increases the resistance of the same, is congealed. Now if that water becomes fluid, it will somewhat increase the resistance. But in these Propositions that increase is so small, that it may be neglected, because the convex superficies of the globe produces the very same effect almost as the congelation of the water.

Let A be the weight of the globe in vacuo, B its weight in the resisting medium, D the diameter of the globe. F a space which is to ⁴/₃D as the density of the globe to the density of the medium, that is, as A to A − B, G the time in which the globe falling with the weight B without resistance describes the space F, and H the velocity which the body acquires by that fall. Then H will be the greatest velocity with which the globe can possibly descend with the weight B in the resisting medium, by Cor. 2, Prop XXXVIII; and the resistance which the globe meets with, when descending with that velocity, will be equal to its weight B; and the resistance it meets with in any other velocity will be to the weight B in the duplicate ratio of that velocity to the greatest velocity H, by Cor. 1, Prop. XXXVIII.

This is the resistance that arises from the inactivity of the matter of the fluid. That resistance which arises from the elasticity, tenacity, and friction of its parts, may be thus investigated.

Let the globe be let fall so that it may descend in the fluid by the weight B; and let P be the time of falling, and let that time be expressed in seconds, if the time G be given in seconds. Find the absolute number N agreeing to the logarithm 0,4342944819 2P
G, and let L be the logarithm of the number N + 1
N; and the velocity acquired in falling will be N − 1
N + 1H, and the height described will be 2PF
G − 1,3862943611F + 4,605170186LF. If the fluid be of a sufficient depth, we may neglect the term 4,605170186LF; and 2PF
G − 1,3862943611F will be the altitude described, nearly. These things appear by Prop. IX, Book II, and its Corollaries, and are true upon this supposition, that the globe meets with no other resistance but that which arises from the inactivity of matter. Now if it really meet with any resistance of another kind, the descent will be slower, and from the quantity of that retardation will be known the quantity of this new resistance.

That the velocity and descent of a body falling in a fluid might more easily be known, I have composed the following table; the first column of which denotes the times of descent; the second shews the velocities acquired in falling, the greatest velocity being 100000000: the third exhibits the spaces described by falling in those times, 2F being the space which the body describes in the time G with the greatest velocity; and the fourth gives the spaces described with the greatest velocity in the same times. The numbers in the fourth column are 2P
G, and by subducting the number 1,3862944 − 4,6051702L, are found the numbers in the third column; and these numbers must be multiplied by the space F to obtain the spaces described in falling. A fifth column is added to all these, containing the spaces described in the same times by a body falling in vacuo with the force of B its comparative weight.

The Times P	Velocities of the body falling in the fluid	The spaces described in falling in the fluid	The spaces described with the greatest motion	The spaces described by falling In vacuo
0,001G 0,01G 0,1G 0,2G 0,3G 0,4G 0,5G 0,6G 0,7G 0,8G 0,9G 1G 2G 3G 4G 5G 6G 7G 8G 9G 10G	9999929/30 999967 9966799 19737532 29131261 37994896 46211716 53704957 60436778 66403677 71629787 76159416 96402758 99505475 99932930 99990920 99998771 99999834 99999980 99999997 999999993/5	0,000001F 0,0001F 0,0099834F 0,0397361F 0,0886815F 0,1559070F 0,2402290F 0,3402706F 0,4545405F 0,5815071F 0,7196609F 0,8675617F 2,6500055F 4,6186570F 6,6143765F 8,6137964F 10,6137179F 12,6137073F 14,6137059F 16,6137057F 18,6137056F	0,002F 0,02F 0,2F 0,4F 0,6F 0,8F 1,0F 1,2F 1,4F 1,6F 1,8F 2F 4F 6F 8F 10F 12F 14F 16F 18F 20F	0,000001F 0,0001F 0,01F 0,04F 0,09F 0,16F 0,25F 0,36F 0,49F 0,64F 0,81F 1F 4F 9F 16F 25F 36F 49F 64F 81F 100F

In order to investigate the resistances of fluids from experiments, I procured a square wooden vessel, whose length and breadth on the inside was 9 inches English measure, and its depth 9 feet ½; this I filled with rainwater: and having provided globes made up of wax, and lead included therein, I noted the times of the descents of these globes, the height through which they descended being 112 inches. A solid cubic foot of English measure contains 76 pounds troy weight of rainwater; and a solid inch contains 19
36 ounces troy weight, or 253⅓ grains; and a globe of water of one inch in diameter contains 132,645 grains in air, or 132,8 grains in vacuo; and any other globe will be as the excess of its weight in vacuo above its weight in water.

Exper. 1. A globe whose weight was 156¼ grains in air, and 77 grains in water, described the whole height of 112 inches in 4 seconds. And, upon repeating the experiment, the globe spent again the very same time of 4 seconds in falling.

The weight of this globe in vacuo is 156 13
38 grains; and the excess of this weight above the weight of the globe in water is 79 13
38 grains. Hence the diameter of the globe appears to be 0,84224 parts of an inch. Then it will be, as that excess to the weight of the globe in vacuo, so is the density of the water to the density of the globe; and so is ⁸/₃ parts of the diameter of the globe (viz. 2,24597 inches) to the space 2F, which will be therefore 4,4256 inches. Now a globe falling in vacuo with its whole weight of 156 13
38 grains in one second of time will describe 193⅓ inches; and falling in water in the same time with the weight of 77 grains without resistance, will describe 95,219 inches; and in the time G, which is to one second of time in the subduplicate ratio of the space F, or of 2,2128 inches to 95,219 inches, will describe 2,2128 inches, and will acquire the greatest velocity H with which it is capable of descending in water. Therefore the time G is 0″.15244. And in this time G, with that greatest velocity H, the globe will describe the space 2F, which is 4,4256 inches; and therefore in 4 seconds will describe a space of 116,1245 inches. Subduct the space 1,3862944F, or 3,0676 inches, and there will remain a space of 113,0569 inches, which the globe falling through water in a very wide vessel will describe in 4 seconds. But this space, by reason of the narrowness of the wooden vessel before mentioned, ought to be diminished in a ratio compounded of the subduplicate ratio of the orifice of the vessel to the excess of this orifice above half a great circle of the globe, and of the simple ratio of the same orifice to its excess above a great circle of the globe, that is, in a ratio of 1 to 0,9914. This done, we have a space of 112,08 inches, which a globe falling through the water in this wooden vessel in 4 seconds of time ought nearly to describe by this theory; but it described 112 inches by the experiment.

Exper. 2. Three equal globes, whose weights were severally 76⅓ grains in air, and 5 ¹/₁₆ grains in water, were let fall successively; and every one fell through the water in 15 seconds of time, describing in its fall a height of 112 inches.

By computation, the weight of each globe in vacuo is 76 5
12 grains; the excess of this weight above the weight in water is 71 grains 17
48; the diameter of the globe 0,81296 of an inch; ⁸/₃ parts of this diameter 2,16789 inches; the space 2F is 2,3217 inches; the space which a globe of 5 ¹/₁₆ grains in weight would describe in one second without resistance, 12,808 inches, and the time G0″,301056. Therefore the globe, with the greatest velocity it is capable of receiving from a weight of 5 ¹/₁₆ grains in its descent through water, will describe in the time 0″,301056 the space of 2,3217 inches; and in 15 seconds the space 115,678 inches. Subduct the space 1,3862944F, or 1,609 indies, and there remains the space 114.069 inches, which therefore the falling globe ought to describe in the same time, if the vessel were very wide. But because our vessel was narrow, the space ought to be diminished by about 0,895 of an inch. And so the space will remain 113,174 inches, which a globe falling in this vessel ought nearly to de scribe in 15 seconds, by the theory. But by the experiment it described 112 inches. The difference is not sensible.

Exper. 3. Three equal globes, whose weights were severally 121 grains in air, and 1 grain in water, were successively let fall; and they fell through the water in the times 46″, 47″, and 50″, describing a height of 112 inches.

By the theory, these globes ought to have fallen in about 40″. Now whether their falling more slowly were occasioned from hence, that in slow motions the resistance arising from the force of inactivity does really bear a less proportion to the resistance arising from other causes; or whether it is to be attributed to little bubbles that might chance to stick to the globes, or to the rarefaction of the wax by the warmth of the weather, or of the hand that let them fall; or, lastly, whether it proceeded from some insensible errors in weighing the globes in the water, I am not certain. Therefore the weight of the globe in water should be of several grains, that the experiment may be certain, and to be depended on.

Exper. 4. I began the foregoing experiments to investigate the resistances of fluids, before I was acquainted with the theory laid down in the Propositions immediately preceding. Afterward, in order to examine the theory after it was discovered, I procured a wooden vessel, whose breadth on the inside was 8⅔ inches, and its depth 15 feet and ⅓. Then I made four globes of wax, with lead included, each of which weighed 139¼ grains in air, and 7 1
8 grains in water. These I let fall, measuring the times of their falling in the water with a pendulum oscillating to half seconds. The globes were cold, and had remained so some time, both when they were weighed and when they were let fall; because warmth rarefies the wax, and by rarefying it diminishes the weight of the globe in the water; and wax, when rarefied, is not instantly reduced by cold to its former density. Before they were let fall, they were totally immersed under water, lest, by the weight of any part of them that might chance to be above the water, their descent should be accelerated in its beginning. Then, when after their immersion they were perfectly at rest, they were let go with the greatest care, that they might not receive any impulse from the hand that let them down. And they fell successively in the times of 47½, 48½, 50, and 51 oscillations, describing a height of 15 feet and 2 inches. But the weather was now a little colder than when the globes were weighed, and therefore I repeated the experiment another day; and then the globes fell in the times of 49; 49½, 50. and 53; and at a third trial in the times of 49½, 50, 51, and 53 oscillations. And by making the experiment several times over, I found that the globes fell mostly in the times of 49½ and 50 oscillations. When they fell slower, I suspect them to have been retarded by striking against the sides of the vessel.

Now, computing from the theory, the weight of the globe in vacuo is 139 2
5 grains; the excess of this weight above the weight of the globe in water 132 11
40 grains; the diameter of the globe 0,99868 of an inch; ⁸/₃ parts of the diameter 2,66315 inches; the space 2F 2,8066 inches; the space which a globe weighing 7 1
8 grains falling without resistance describes in a second of time 9,88164 inches; and the time GO″,376843. Therefore the globe with the greatest velocity with which it is capable of descending through the water by the force of a weight of 7 1
8 grains, will in the time 0″,376843 describe a space of 2,8066 inches, and in one second of time a space of 7,44766 inches, and in the time 25″, or in 50 oscillations, the space 186,1915 inches. Subduct the space 1,386294F, or 1,9454 inches, and there will remain the space 184,2461 inches which the globe will describe in that time in a very wide vessel. Because our vessel was narrow, let this space be diminished in a ratio compounded of the subduplicate ratio of the orifice of the vessel to the excess of this orifice above half a great circle of the globe, and of the simple ratio of the same orifice to its excess above a great circle of the globe; and we shall have the space of 181,86 inches, which the globe ought by the theory to describe in this vessel in the time of 50 oscillations, nearly. But it described the space of 182 inches, by experiment, in 49½ or 50 oscillations.

Exper. 5. Four globes weighing 154³/₈ grains in air, and 21½ grains in water, being let fall several times, fell in the times of 28½, 29, 29½, and 30, and sometimes of 31, 32, and 33 oscillations, describing a height of 15 feet and 2 inches.

They ought by the theory to have fallen in the time of 29 oscillations, nearly.

Exper. 6. Five globes, weighing 212 ⅜ grains in air, and 79½ in water, being several times let fall, fell in the times of 15, 15½, 16, 17, and 18 oscillations, describing a height of 15 feet and 2 inches.

By the theory they ought to have fallen in the time of 15 oscillations, nearly.

Exper. 7. Four globes, weighing 293³/₈ grains in air, and 35 ⁷/₈ grains in water, being let fall several times, fell in the times of 29½, 30, 30½, 31, 32, and 33 oscillations, describing a height of 15 feet and 1 inch and ½.

By the theory they ought to have fallen in the time of 28 oscillations, nearly.

In searching for the cause that occasioned these globes of the same weight and magnitude to fall, some swifter and some slower, I hit upon this; that the globes, when they were first let go and began to fall, oscillated about their centres; that side which chanced to be the heavier descending first, and producing an oscillating motion. Now by oscillating thus, the globe communicates a greater motion to the water than if it descended without any oscillations; and by this communication loses part of its own motion with which it should descend; and therefore as this oscillation is greater or less, it will be more or less retarded. Besides, the globe always recedes from that side of itself which is descending in the oscillation, and by so receding comes nearer to the sides of the vessel, so as even to strike against them sometimes. And the heavier the globes are, the stronger this oscillation is; and the greater they are, the more is the water agitated by it. Therefore to diminish this oscillation of the globes, I made new ones of lead and wax, sticking the lead in one side of the globe very near its surface; and I let fall the globe in such a manner, that, as near as possible, the heavier side might be lowest at the beginning of the descent. By this means the oscillations became much less than before, and the times in which the globes fell were not so unequal: as in the following experiments.

Exper. 8. Four globes weighing 139 grains in air, and 6½ in water, were let fall several times, and fell mostly in the time of 51 oscillations, never in more than 52, or in fewer than 50, describing a height of 182 inches.

By the theory they ought to fall in about the time of 52 oscillations

Exper. 9. Four globes weighing 273¼ grains in air, and 140¾ in water, being several times let fall, fell in never fewer than 12, and never more than 13 oscillations, describing a height of 182 inches.

These globes by the theory ought to have fallen in the time of 11⅓ oscillations, nearly.

Exper. 10. Four globes, weighing 384 grains in air, and 119½ in water, being let fall several times, fell in the times of 17¾ 18, 18½, and 19 oscillations, describing a height of 181½ inches. And when they fell in the time of 19 oscillations, I sometimes heard them hit against the sides of the vessel before they reached the bottom.

By the theory they ought to have fallen in the time of 15⁵/₉ oscillations, nearly.

Exper. 11. Three equal globes, weighing 48 grains in the air, and 3 29
32 in water, being several times let fall, fell in the times of 43½, 44, 44½, 45, and 46 oscillations, and mostly in 44 and 45, describing a height of 182½ inches, nearly.

By the theory they ought to have fallen in the time of 46 oscillations and⁵/₉, nearly.

Exper. 12. Three equal globes, weighing 141 grains in air, and 4³/₈ in water, being let fall several times, fell in the times of 61, 62, 63, 64, and 65 oscillations, describing a space of 182 inches.

And by the theory they ought to have fallen in 64½ oscillations nearly.

From these experiments it is manifest, that when the globes fell slowly, as in the second, fourth, fifth, eighth, eleventh, and twelfth experiments, the times of falling are rightly exhibited by the theory; but when the globes fell more swiftly, as in the sixth, ninth, and tenth experiments, the resistance was somewhat greater than in the duplicate ratio of the velocity. For the globes in falling oscillate a little; and this oscillation, in those globes that are light and fall slowly, soon ceases by the weakness of the motion; but in greater and heavier globes, the motion being strong, it continues longer, and is not to be checked by the ambient water till after several oscillations. Besides, the more swiftly the globes move, the less are they pressed by the fluid at their hinder parts; and if the velocity be perpetually increased, they will at last leave an empty space behind them, unless the compression of the fluid be increased at the same time. For the compression of the fluid ought to be increased (by Prop. XXXII and XXXIII) in the duplicate ratio of the velocity, in order to preserve the resistance in the same duplicate ratio. But because this is not done, the globes that move swiftly are not so much pressed at their hinder parts as the others; and by the defect of this pressure it comes to pass that their resistance is a little greater than in a duplicate ratio of their velocity.

So that the theory agrees with the phaenomena of bodies falling in water. It remains that we examine the phaenomena of bodies falling in air.

Exper. 13. From the top of St. Paul's Church in London, in June 1710, there were let fall together two glass globes, one full of quicksilver, the other of air; and in their fall they described a height of 220 English feet. A wooden table was suspended upon iron hinges on one side, and the other side of the same was supported by a wooden pin. The two globes lying upon this table were let fall together by pulling out the pin by means of an iron wire reaching from thence quite down to the ground; so that, the pin being removed, the table, which had then no support but the iron hinges, fell downward, and turning round upon the hinges, gave leave to the globes to drop off from it. At the same instant, with the same pull of the iron wire that took out the pin, a pendulum oscillating to seconds was let go, and began to oscillate. The diameters and weights of the globes, and their times of falling, are exhibited in the following table.

The globes filled with mercury			The globes full of air
Weights	Diameters	Times in falling	Weights	Diameters	Times in falling
908 grains 983 grains 866 grains 747 grains 808 grains 784 grains	0,8 of an inch 0,8 of an inch 0,8 of an inch 0,75 of an inch 0,75 of an inch 0,75 of an inch	4″ 4- 4 4+ 4 4+	510 grains 642 grains 599 grains 515 grains 483 grains 641 grains	5,1 inches 5,2 inches 5,1 inches 5,0 inches 5,0 inches 5,2 inches	8″½ 8 8 8¼ 8½ 8

But the times observed must be corrected; for the globes of mercury (by Galileo's theory), in 4 seconds of time, will describe 257 English feet, and 220 feet in only 3″ 42‴. So that the wooden table, when the pin was taken out, did not turn upon its hinges so quickly as it ought to have done; and the slowness of that revolution hindered the descent of the globes at the beginning. For the globes lay about the middle of the table, and indeed were rather nearer to the axis upon which it turned than to the pin. And hence the times of falling were prolonged about 18‴; and therefore ought to be corrected by subducting that excess, especially in the larger globes, which, by reason of the largeness of their diameters, lay longer upon the revolving table than the others. This being done, the times in which the six larger globes fell will come forth 8″ 12‴, 7″ 42‴, 7″ 42‴, 7″ 57‴, 8″ 12‴ and 7″ 42‴.

Therefore the fifth in order among the globes that were full of air being 5 inches in diameter, and 483 grains in weight, fell in 8″ 12‴, describing a space of 220 feet. The weight of a bulk of water equal to this globe is 16600 grains; and the weight of an equal bulk of air is 16600
860 grains, or 19³/₁₀ grains; and therefore the weight of the globe in vacua is 502³/₁₀ grains; and this weight is to the weight of a bulk of air equal to the globe as 502³/₁₀ to 19³/₁₀; and so is 2F to ⁸/₃ of the diameter of the globe, that is, to 13⅓ inches. Whence 2F becomes 28 feet 11 inches. A globe, falling in vacua with its whole weight of 502³/₁₀ grains, will in one second of time describe 193⅓ inches as above; and with the weight of 483 grains will describe 185,905 inches; and with that weight 483 grains in vacua will describe the space F, or 14 feet 5½ inches, in the time of 57‴ 58″″, and acquire the greatest velocity it is capable of descending with in the air. With this velocity the globe in 8″ 12‴ of time will describe 245 feet and 5⅓ inches. Subduct 1,3863F, or 20 feet and ½ an inch, and there remain 225 feet 5 inches. This space, therefore, the falling globe ought by the theory to describe in 8″ 12‴. But by the experiment it described a space of 220 feet. The difference is insensible.

By like calculations applied to the other globes full of air, I composed the following table.

The weights of the globe	The diameters	The times falling from a height of 220 feet	The spaces which they would describe by the theory	The excesses
510 grains 642 grains 599 grains 515 grains 483 grains 641 grains	5,1 inches 5,2 inches 5,1 inches 5 inches 5 inches 5,2 inches	8″ 12‴ 7″ 42‴ 7″ 42‴ 7″ 57‴ 8″ 12‴ 7″ 42‴	226 feet 11 inch. 230 feet 9 inch. 227 feet 10 inch. 224 feet 5 inch. 225 feet 5 inch 230 feet 7 inch.	6 feet 11 inch 10 feet 9 inch 7 feet 0 inch 4 feet 5 inch 5 feet 5 inch 10 feet 7 inch

Exper. 14. Anno 1719, in the month of July, Dr. Desaguliers made some experiments of this kind again, by forming hogs' bladders into spherical orbs; which was done by means of a concave wooden sphere, which the bladders, being wetted well first, were put into. After that being blown full of air, they were obliged to fill up the spherical cavity that contained them; and then, when dry, were taken out. These were let fall from the lantern on the top of the cupola of the same church, namely, from a height of 272 feet; and at the same moment of time there was let fall a leaden globe, whose weight was about 2 pounds troy weight. And in the mean time some persons standing in the upper part of the church where the globes were let fall observed the whole times of falling; and others standing on the ground observed the differences of the times between the fall of the leaden weight and the fall of the bladder. The times were measured by pendulums oscillating to half seconds. And one of those that stood upon the ground had a machine vibrating four times in one second; and another had another machine accurately made with a pendulum vibrating four times in a second also. One of those also who stood at the top of the church had a like machine; and these instruments were so contrived, that their motions could be stopped or renewed at pleasure. Now the leaden globe fell in about four seconds and ¼ of time; and from the addition of this time to the difference of time above spoken of, was collected the whole time in which the bladder was falling. The times which the five bladders spent in falling, after the leaden globe had reached the ground, were, the first time, 14¾″, 12¾″, 14⁵/₈″, 17¾″, and 16⁷/₈″; and the second time, 14½″, 14¼″, 14″, 19″, and 16¾″. Add to these 4¼″, the time in which the leaden globe was falling, and the whole times in which the five bladders fell were, the first time, 19″, 17″, 18⁷/₈″, 22″, and 21¹/₈″; and the second time, 18¾″, 18½″, 18¼″, 23¼″, and 21″. The times observed at the top of the church were, the first time, 19³/₈″, 17¼″, 18¾″, 22¹/₈″, and 21⁵/₈″; and the second time, 19″, 18⁵/₈″, 18³/₈″, 24″, and 21¼″. But the bladders did not always fall directly down, but sometimes fluttered a little in the air, and waved to and fro, as they were descending. And by these motions the times of their falling were prolonged, and increased by half a second sometimes, and sometimes by a whole second. The second and fourth bladder fell most directly the first time, and the first and third the second time. The fifth bladder was wrinkled, and by its wrinkles was a little retarded. I found their diameters by their circumferences measured with a very fine thread wound about them twice. In the following table I have compared the experiments with the theory; making the density of air to be to the density of rain-water as 1 to 860, and computing the spaces which by the theory the globes ought to describe in falling.

The weight of the bladders	The diameters	The times of falling from a height of 272 feet	The spaces which by the theory ought to have been described in those times	The difference between the theory and the experiments
128 grains 156 grains 137½ grains 97½ grains 991/8 grains	5,28 inches 5,19 inches 5,3 inches 5,26 inches 5 inches	19″ 17″ 18″ 22″ 211/8″	271 feet 11 in. 272 feet 0½ in. 272 feet 7 in. 277 feet 4 in. 282 feet 0 in.	- 0 ft 1 in. + 0 ft 0½ in. + 0 ft 7 in. + 5 ft 4 in. + 10 ft 0 in.

Our theory, therefore, exhibits rightly, within a very little, all the resistance that globes moving either in air or in water meet with; which appears to be proportional to the densities of the fluids in globes of equal velocities and magnitudes.

In the Scholium subjoined to the sixth Section, we shewed, by experiments of pendulums, that the resistances of equal and equally swift globes moving in air, water, and quicksilver, are as the densities of the fluids. We here prove the same more accurately by experiments of bodies falling in air and water. For pendulums at each oscillation excite a motion in the fluid always contrary to the motion of the pendulum in its return; and the resistance arising from this motion, as also the resistance of the thread by which the pendulum is suspended, makes the whole resistance of a pendulum greater than the resistance deduced from the experiments of falling bodies. For by the experiments of pendulums described in that Scholium, a globe of the same density as water in describing the length of its semidiameter in air would lose the 1
3342 part of its motion. But by the theory delivered in this seventh Section, and confirmed by experiments of falling bodies, the same globe in describing the same length would lose only a part of its motion equal to 1
4586, supposing the density of water to be to the density of air as 860 to 1. Therefore the resistances were found greater by the experiments of pendulums (for the reasons just mentioned) than by the experiments of falling globes; and that in the ratio of about 4 to 3. Bat yet since the resistances of pendulums oscillating in air, water, and quicksilver, are alike increased by like causes, the proportion of the resistances in these mediums will be rightly enough exhibited by the experiments of pendulums, as well as by the experiments of falling bodies. And from all this it may be concluded, that the resistances of bodies, moving in any fluids whatsoever, though of the most extreme fluidity, are, caeteris paribus, as the densities of the fluids.

These things being thus established, we may now determine what part of its motion any globe projected in any fluid whatsoever would nearly lose in a given time. Let D be the diameter of the globe, and V its velocity at the beginning of its motion, and T the time in which a globe with the velocity V can describe in vacuo a space that is, to the space ⁸/₃D as the density of the globe to the density of the fluid; and the globe projected in that fluid will, in any other time t lose the part tV
T+t, the part TV
T+t remaining; and will describe a space, which will be to that described in the same time in vacuo with the uniform velocity V, as the logarithm of the number T+t
T multiplied by the number 2,302585093 is to the number t
T, by Cor. 7, Prop. XXXV. In slow motions the resistance may be a little less, because the figure of a globe is more adapted to motion than the figure of a cylinder described with the same diameter. In swift motions the resistance may be a little greater, because the elasticity and compression of the fluid do not increase in the duplicate ratio of the velocity. But these little niceties I take no notice of.

And though air, water, quicksilver, and the like fluids, by the division of their parts in infinitum, should be subtilized, and become mediums infinitely fluid, nevertheless, the resistance they would make to projected globes would be the same. For the resistance considered in the preceding Propositions arises from the inactivity of the matter; and the inactivity of matter is essential to bodies, and always proportional to the quantity of matter. By the division of the parts of the fluid the resistance arising from the tenacity and friction of the parts may be indeed diminished; but the quantity of matter will not be at all diminished by this division; and if the quantity of matter be the same, its force of inactivity will be the same; and therefore the resistance here spoken of will be the same, as being always proportional to that force. To diminish this resistance, the quantity of matter in the spaces through which the bodies move must be diminished; and therefore the celestial spaces, through which the globes of the planets and comets are perpetually passing towards all parts, with the utmost freedom, and without the least sensible diminution of their motion, must be utterly void of any corporeal fluid, excepting, perhaps, some extremely rare vapours and the rays of light.

Projectiles excite a motion in fluids as they pass through them, and this motion arises from the excess of the pressure of the fluid at the fore parts of the projectile above the pressure of the same at the hinder parts; and cannot be less in mediums infinitely fluid than it is in air, water, and quicksilver, in proportion to the density of matter in each. Now this excess of pressure does, in proportion to its quantity, not only excite a motion in the fluid, but also acts upon the projectile so as to retard its motion; and therefore the resistance in every fluid is as the motion excited by the projectile in the fluid; and cannot be less in the most subtile aether in proportion to the density of that aether, than it is in air, water, and quicksilver, in proportion to the densities of those fluids.